Charlie Reid

Hi! I'm a mathematician interested in topics in differential geometry and quantum field theory. Recently I have worked on problems concerning character varieties of surfaces, in particular Hitchin components and their compactifications.

Currently, I have a postdoc at Yale University. Previously I did a postdoc at MPI-MiS in Leipzig, and before that I got my PhD from UT Austin, with a visit to Harvard, advised by Jeffrey Danciger and Dan Freed.

Preprints

• ▶

  Boundary Currents of Hitchin Components

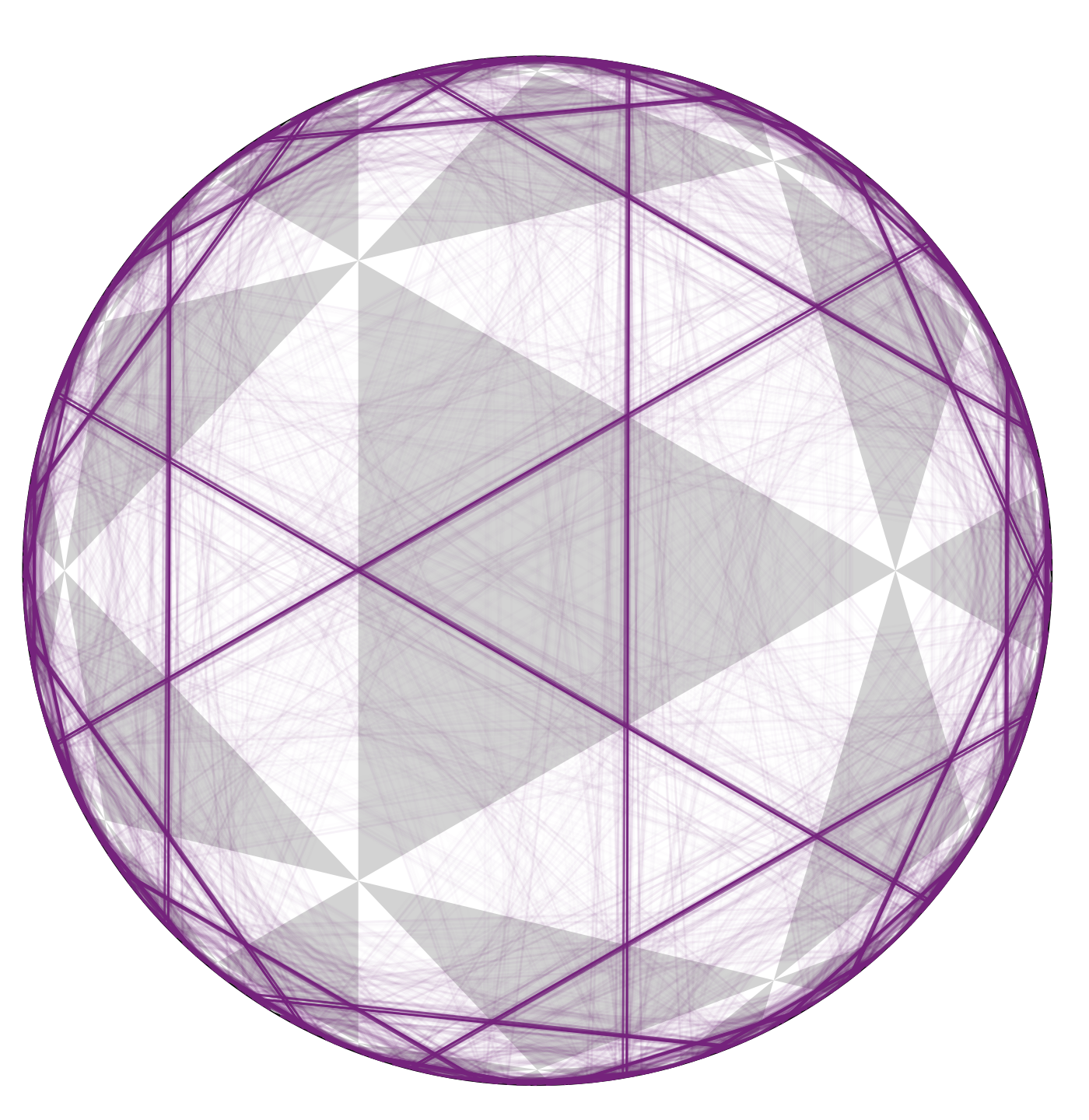
  Measured laminations lie at the boundary of Teichmüller space. What geodesic currents do we find in higher rank? Here is a rough depiction of Liouville currents associated with SL(3, R) Hitchin representations of the 444-triangle reflection group.

  

  Here is one of these currents depicted on the universal cover:

  

  You can see some self-intersections. In my paper I find self-intersection conditions that limits of Liouville currents of Hitchin representations satisfy, and develop a notion of dual space to a geodesic current which works well for these limit currents.

• ▶

  Fock Bundles and Hitchin Components (joint with Alex Thomas and Georgios Kydonakis)

  We define a correspondence between higher complex structures on a smooth surface, and real representations of its fundamental group, and show that the correspondence induces a map of moduli spaces in a neighborhood of the Fuchsian locus.

• ▶

  Limits of Convex Projective Surfaces and Finsler Metrics

  The dots in the picture below are elements of the 444 triangle reflection group of length at most 20. The x and y axes are the logarithms of the top and bottom eigenvalues of these elements under SL(3, R) Hitchin representations. You can see the dots collecting onto a lattice as the representation goes to infinity. This paper gives a geometric way of telling which lattice point a group element will limit to.

  

• ▶

  Symmetries of 2d TQFTs and Equivariant Verlinde Formulae for General Groups (joint with Ali Shehper, Du Pei, and Sergei Gukov)

  We use the concept of higher symmetry gauging to calculate equivariant Verlinde formulae for non simply connected groups.

Other Stuff

• ▶

  Arbeitsgemeinschaft: Higher Rank Teichmüller Theory (Oberwolfach Report)

  I gave the talk titled "Universal Higher Teichmüller Spaces" of the 2022 Oberwolfach Arbeitsgemeinschaft titled Higher Rank Teichmüller Theory. You can find my extended abstract at the end of the report.

• ▶

  Differential Cohomology: Categories, Characteristic Classes, and Connections (by Arun Debray, Araminta Amabel, and Peter Haine)

  I participated in a seminar on differential cohomology which eventually led to this book. I gave the conformal immersions talk, so I wrote the first draft of chapter 20, but it is mostly new content now.

• ▶

  Overruled Lagrangian Cones: Origins and Incarnations (Undergraduate Thesis)

  Advised by Alexander Givental. I'm not exactly sure how correct it is, but it is amusing to see this material from the perspective of an undergrad. Some of it could be useful.